Polyhedron: Difference between revisions
imported>Anthony Argyriou (add images and data to table) |
imported>Anthony Argyriou (redo table as a gallery) |
||
| Line 4: | Line 4: | ||
The polygons bounding a polyhedron are known as faces; the line segments bounding the polygons are known as edges, and the points where the faces meet are vertices (singular vertex). | The polygons bounding a polyhedron are known as faces; the line segments bounding the polygons are known as edges, and the points where the faces meet are vertices (singular vertex). | ||
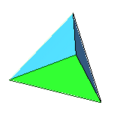
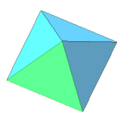
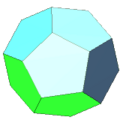
A convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a [[Platonic solid]]. There are only five Platonic solids, shown | A convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a [[Platonic solid]]. There are only five Platonic solids, shown below: | ||
<gallery> | |||
Image:Tetrahedron.png|[[regular tetrahedron]]:4 [[triangle]] faces, 4 vertices, 6 edges | |||
Image:Cube.png|[[cube]]: 6 [[square]] faces, 8 vertices, 12 edges | |||
Image:Octahedron.png|[[regular octahedron]]: 8 [[triangle]] faces, 6 vertices, 12 edges | |||
Image:Dodecahedron.png|[[regular dodecahedron]]: 12 [[pentagon]] faces, 20 vertices, 30 edges | |||
Image:Icosahedron.png|[[regular icosahedron]]: 20 [[triangle]] faces, 12 vertices, 30 edges | |||
|[[regular tetrahedron]] | </gallery> | ||
|[[cube]] | |||
|[[regular octahedron]] | |||
|[[regular dodecahedron]] | |||
|[[regular icosahedron]] | |||
Revision as of 00:15, 15 October 2008
A polyhedron is a three-dimensional geometric closed figure bounded by a connected set of polygons. A polyhedron, in Euclidian geometry, must have at least four faces. A polyhedron of four sides is called a tetrahedron, six sides a hexahedron, eight sides an octahedron, ten sides a decahedron. Figures with more sides are typically named with the Greek name for the number of sides, followed by "-hedron".
The polygons bounding a polyhedron are known as faces; the line segments bounding the polygons are known as edges, and the points where the faces meet are vertices (singular vertex).
A convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a Platonic solid. There are only five Platonic solids, shown below:
regular tetrahedron:4 triangle faces, 4 vertices, 6 edges
regular octahedron: 8 triangle faces, 6 vertices, 12 edges
regular dodecahedron: 12 pentagon faces, 20 vertices, 30 edges
regular icosahedron: 20 triangle faces, 12 vertices, 30 edges