Boiling point

The boiling point of a liquid is the temperature at which the vapor pressure of the liquid equals the external environmental pressure surrounding the liquid. The boiling point of a liquid may also be defined as the temperature at which it changes state from a liquid to a gas throughout the bulk of the liquid. At that point, bubbles of vapor which form below the surface of the liquid contain vapor at a pressure which matches the external pressure. Therefore, they are not crushed by the surrounding liquid and their buoyancy causes them to rise through to the surface of the liquid and give the familiar appearance of a boiling liquid.

A liquid in a vacuum environment has a lower boiling point than when the liquid is at atmospheric pressure. A liquid in a high pressure environment has a higher boiling point than when the liquid is at atmospheric pressure. In other words, the boiling point of a liquid varies with and depends upon the surrounding environmental pressure. The boiling point increases with increased pressure up to the critical point, where the gas and liquid properties become identical. The boiling point cannot be increased beyond the critical point. Likewise, the boiling point decreases with decreasing pressure until the triple point is reached. The boiling point cannot be reduced below the triple point.

Liquids may change to a vapor at temperatures below their boiling points through the process of evaporation. Evaporation is a surface phenomenon in which molecules located near the vapor/liquid surface escape into the vapor phase. On the other hand, boiling is a process in which molecules anywhere in the liquid escape, resulting in the formation of vapor bubbles within the liquid.

The normal boiling point

The normal boiling point (also called the atmospheric boiling point or the atmospheric pressure boiling point) of a liquid is the special case in which the vapor pressure of the liquid equals 101.325 kilopascals (kPa).

Usually, boiling points are published with respect to the atmospheric pressure (101.325 kPa or 1 atm) at sea level, which is also known as the standard atmosphere. In other words, published boiling points of liquids are usually the normal boiling points of the liquids.

Calculation of the normal boiling point

The heat of vaporization is the amount of heat required to convert or vaporize a saturated liquid (i.e., a liquid at its boiling point) into a vapor.

If the heat of vaporization and the vapor pressure of a liquid at a certain temperature is known, the normal boiling point can be calculated by using this form of the Clausius-Clapeyron equation:

$T_{B}={\Bigg (}{\frac {\,R\,[\,\ln(P_{0})-\ln(101.325)\,]}{\Delta H_{vap}}}+{\frac {1}{T_{0}}}{\Bigg )}^{-1}$

where:
$T_{B}$	= the normal boiling point, K
$R$	= the molar gas constant, 8.314 J · K-1 · mol-1
$P_{0}$	= is the vapor pressure at a given temperature, kPa
$101.325$	= atmospheric pressure, kPa
$\Delta H_{vap}$	= the heat of vaporization of the liquid, J/mol
$T_{0}$	= the given temperature, K
$ln$	= the natural logarithm to the base e

Saturation temperature and pressure

A saturated liquid contains as much thermal energy (i.e., heat) as it can without boiling and, conversely, a saturated vapor contains as little thermal energy as it can without condensing.

The term saturation temperature means boiling point and it is the temperature for a corresponding saturation pressure at which a liquid boils into its vapor phase. The liquid can be said to be saturated with thermal energy. Any addition of thermal energy results in a phase change.

If the pressure in a system remains constant (i.e., the system is isobaric), a vapor at saturation temperature will begin to condense into its liquid phase as thermal energy is removed. Similarly, a liquid at saturation temperature and pressure will boil into its vapor phase as additional thermal energy is applied.

The saturation pressure is the pressure for a corresponding saturation temperature at which a liquid boils into its vapor phase. Saturation pressure and saturation temperature have a direct relationship: as saturation pressure is increased so is saturation temperature.

If the temperature in a system remains constant (i.e., the system is isothermal), vapor at saturation pressure and temperature will begin to condense into its liquid phase as the system pressure is increased. Similarly, a liquid at saturation pressure and temperature will tend to boil into its vapor phase as the system pressure is decreased.

Relation between the normal boiling point and the vapor pressure of liquids

A typical vapor pressure chart for various liquids

The higher is the vapor pressure of a liquid at a given temperature, the lower the normal boiling point of the liquid.

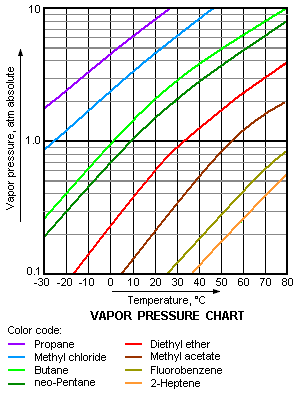
The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids. As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points.

For example, at any given temperature, propane has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (–42.1 °C), which is where the vapor pressure curve of propane (the purple line) intersects the horizontal pressure line of one atmosphere (1 atm) of absolute vapor pressure.

In terms of intermolecular forces, the boiling point represents the point at which the liquid molecules possess enough thermal energy to overcome the various intermolecular attractions binding the molecules into the liquid. Therefore the boiling point is also an indicator of the strength of those attractive forces. The higher the intermolecular attractive forces are, the more difficult it is for molecules to escape from the liquid and hence the lower is the vapor pressure of the liquid. The lower the vapor pressure of the liquid, the higher the temperature must be to initiate boiling. Thus, the higher the intermolecular attractive forces are, the higher is the normal boiling point.