Tetration: Difference between revisions
imported>Dmitrii Kouznetsov (add pic) |
imported>Dmitrii Kouznetsov |
||
| Line 7: | Line 7: | ||
<math>x</math>.]] | <math>x</math>.]] | ||
This article is currently [[under construction]]. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration | This article is currently [[under construction]]. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration | ||
== | ==Definiton== | ||
For real <math>b>1</math>, Tetration <math>F=\mathrm{tet}_b</math> on the base <math>b</math> is function of complex variable, which is [[holomorphic]] at least in the range | |||
<math> \{ z \in \mathbb{C} :~ \Re(z) > -2 \}</math>, bounded in the range | |||
<math> \{ z \in \mathbb{C} :~ |\Re(z)| \le 1 \}</math>, and satisfies conditions | |||
: <math> F(z+1) = \exp_b\! \big( F(z) \big) </math> | |||
: <math> F(0) = 1 </math> | |||
: <math> F\!\big(z^*\big) = F\big(z\big)^*</math> | |||
at least within range <math> \Re(z)>-2 </math>. | |||
==Real values of the arguments== | |||
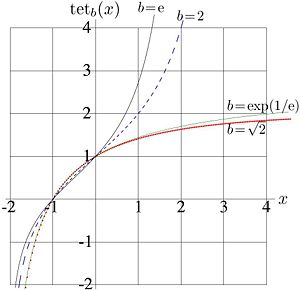
Examples of behavior of this function at the real axis are shown in figure 1 for values | |||
<math>b=\mathrm{e}</math>, | |||
<math>b=2</math>, | |||
<math>b=\exp(1/\mathrm{e})</math>, and for | |||
<math>b=\sqrt{2}</math>. It has logarithmic singularity at <math>-2</math>, and it is monotonously increasing function. | |||
At <math>b\le \exp(1/\mathrm{e})</math> tetration <math>\mathrm{tet}_b(x)</math> approaches its limiting value as | |||
<math>x\rightarrow +\infty</math>, and <math>\displaystyle \lim_{x \rightarrow +\infty} ~ \mathrm{tet}_b(x) > 1</math>. | |||
At <math>b > \exp(1/\mathrm{e})</math> tetration <math>\mathrm{tet}_b(x)</math> grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in [[mathematics of computation]]. | |||
A number, that cannot be stored as [[floating point]], could be stored as <math>\mathrm{tet}_b(x)</math> for some standard value of <math>b</math> (for example, <math>b=2</math> or <math>b=\mathrm{e}</math>) and relatively moderate value of <math>x</math>. The analytic properties of tetration could be used for the implementation of arithmetic operations without to convert numbers to the floating point representation. | |||
==Integer values of the argument== | |||
For integer <math>z</math>, tetration | |||
: <math>{\rm tet}_b</math> | |||
==Etymology== | ==Etymology== | ||
Revision as of 06:34, 29 October 2008
This article is currently under construction. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration
Definiton
For real Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b>1} , Tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\mathrm{tet}_b} on the base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is function of complex variable, which is holomorphic at least in the range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ z \in \mathbb{C} :~ \Re(z) > -2 \}} , bounded in the range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ z \in \mathbb{C} :~ |\Re(z)| \le 1 \}} , and satisfies conditions
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z+1) = \exp_b\! \big( F(z) \big) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(0) = 1 }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F\!\big(z^*\big) = F\big(z\big)^*}
at least within range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Re(z)>-2 } .
Real values of the arguments
Examples of behavior of this function at the real axis are shown in figure 1 for values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\mathrm{e}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=2} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\exp(1/\mathrm{e})} , and for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\sqrt{2}} . It has logarithmic singularity at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2} , and it is monotonously increasing function.
At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\le \exp(1/\mathrm{e})} tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b(x)} approaches its limiting value as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow +\infty} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \lim_{x \rightarrow +\infty} ~ \mathrm{tet}_b(x) > 1} .
At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b > \exp(1/\mathrm{e})} tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b(x)} grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation. A number, that cannot be stored as floating point, could be stored as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b(x)} for some standard value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} (for example, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=2} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\mathrm{e}} ) and relatively moderate value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . The analytic properties of tetration could be used for the implementation of arithmetic operations without to convert numbers to the floating point representation.
Integer values of the argument
For integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , tetration
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm tet}_b}
Etymology
Creation of word tetration is attributed to Englidh mathematician Reuben Louis Goodstein [1] [2].
Piecewice tetration
uxp
Analytic tetration
This section is not yet written. There is non-finished draft at User:Dmitrii Kouznetsov/Analytic Tetration.
Inverse of tetration
See also
References
- ↑ "TETRATION, a term for repeated exponentiation, was introduced by Reuben Louis Goodstein". Earliest Known Uses of Some of the Words of Mathematics, http://members.aol.com/jeff570/t.html
- ↑ R.L.Goodstein (1947). "Transfinite ordinals in recursive number theory". Journal of Symbolic Logic 12.
Free online sources
- http://reglos.de/lars/ffx.html , Lars Kindermann. References about Iterative Roots and Fractional Iteration.
- http://math.eretrandre.org/tetrationforum/index.php , Discussion about tetration
- http://tetration.itgo.com/ Tetration site by Andrew Robbins
- http://www.tetration.org/ Tetration site by Daniel Geisler