Limit of a function: Difference between revisions
imported>Igor Grešovnik No edit summary |
imported>Johan Förberg (Added graph of (1+ 1/n)^n) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
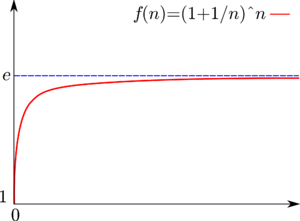
{{Image|Plot-e.png|right|300px|The function <math>(1 + \tfrac{1}{n})^n</math> tends towards <math>e</math> as <math>x</math> tends towards infinity.}} | |||
In [[mathematics]], the concept of a '''limit''' is used to describe the behavior of a [[function (mathematics)|function]] as its [[argument]] either "gets close" to some point, or as it becomes arbitrarily large. | In [[mathematics]], the concept of a '''limit''' is used to describe the behavior of a [[function (mathematics)|function]] as its [[argument]] either "gets close" to some point, or as it becomes arbitrarily large. | ||
Revision as of 14:11, 30 September 2010
In mathematics, the concept of a limit is used to describe the behavior of a function as its argument either "gets close" to some point, or as it becomes arbitrarily large.
Suppose f(x) is a real-valued function and a is a real number. The expression
means that f(x) can be made arbitrarily close to L by making x sufficiently close to a. We say that "the limit of the function f of x, as x approaches a, is L".
Limit of a function can in some cases be defined even at values of the argument at which the function itself is not defined. For example,
although the function
is not defined at x=0.
Formal definition
Let f be a function defined on an open interval containing a (except possibly at a) and let L be a real number.
means that
- for each real ε > 0 there exists a real δ > 0 such that for all x with 0 < |x − a| < δ, we have |f(x) − L| < ε.
This formal definition of function limit is due to the German mathematician Karl Weierstrass.