Interspike interval histogram: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>Subpagination Bot
m (Add {{subpages}} and remove any categories (details))
imported>Daniel Mietchen
m (intralinks)
 
(14 intermediate revisions by 5 users not shown)
Line 3: Line 3:
An '''interspike-interval histogram''' is one of the ways by which experimental neurophysiologists analyse the electrical behaviour of [[neuron]]s in the brain.
An '''interspike-interval histogram''' is one of the ways by which experimental neurophysiologists analyse the electrical behaviour of [[neuron]]s in the brain.


One of the most important ways by which neurons in the brain carry information is by means of electrical signals. At rest, neurons have a ‘resting membrane potential’ of typically about -70 mV: this is the potential difference between the inside of the cell and the external environment. However, this membrane potential is continually being disturbed by the chemical signals released by other neurons. In the brain a neuron might be receiving inputs from as many as ten thousand other neurons, these inputs usually consist of brief excitations (EPSPs; excitatory post-synaptic potentials) or of brief inhibitions (IPSPs; inhibitory post-synaptic potentials) that either make the membrane less negative (depolarisations) or more negative (hyperpolarisations). If a neuron becomes sufficiently depolarised, perhaps because of a flurry of EPSPs, then the membrane potential may reach the critical threshold for triggering an action potential (commonly called a ‘’spike’’). An action potential is a very large and rapid rise in the cell membrane potential, that lasts for only about one millisecond before the membrane potential returns again to around its resting potential. These spikes are propagated along the axons of a neuron, to reach the nerve terminals, where they can trigger the release of chemical messengers to affect other neurons.
One of the simplest ways to study the patterning of [[action potential|spike activity]] in a neuron is to record the spikes from a single neuron, using a fine [[microelectrode]], and then to construct an interspike interval histogram. This is simply a plot of the distribution of the observed [[interspike interval|times between spikes]] (t1, t2, t3, etc) collected in ‘bins’ of fixed width, say 1 ms. Typically, such a histogram would be constructed from about 2000 such intervals; if a neuron is firing at an average rate of about 5 spikes/s this will need a recording of 5-10 min of activity.
[[Image:Spiketimes.png|thumb|300 px| Schematic showing measurement of successive intervals (t1, t2, t3, etc) between successive spikes of electrical activity recorded from a neuron]]
[[Image:ISIH.png|thumb|300 px| Interspike interval distribution of the spontaneous activity of a typical magnocellular [[oxytocin]] neuron recorded from the rat [[supraoptic nucleus]]. The curve is a single negative exponential curve fitted to the tail of the histogram.]]
Thus spikes are a very important way by which neurons in the brain carry information. The spike itself is an all-or-none phenomenon, so information is coded not in the amplitude of a spike but in the timing of spikes. Accordingly, electrophysiologists, who study the electrical behaviour of neurons, are interested in the patterning of spikes in particular neurons. The patterning of spike activity is influenced by three things:
The figure on the right shows the interspike interval histogram recorded from a single neuron in the [[hypothalamus]]. Immediately after a spike, a neuron has an absolute refractory period in which it is unable to fire another spike, so the first few bins of the histogram will be empty – the histogram starts from zero. After this, the neuron has a relative refractory period, during which it is hard, but not impossible, to trigger another spike, and as this relative [[refractory period]] gradually decays, the interspike interval distribution rises to its peak value – the mode of the histogram, in this example at about 50 ms. The tail of the histogram (from about 50 ms on) declines exponentially to zero, as shown by the fitted line. This exponentially declining tail is an indication that, after about 50 ms after a spike, spikes are triggered by an essentially random process. This follows because the distribution of inter-event times for a wholly random process fits a single negative exponential, as first observed by [[Simeon Denis Poisson|Poisson]].
a) the intrinsic properties of the neuron, especially the properties of its membrane. The neurons in the brain are very diverse; there are very many different subpopulations of neurons that have quite different intrinsic properties
b) network interactions, because spike activity in one neuron might have feedback effects on that neuron because of the changes that it produces in reciprocally connected neurons
and
c) the nature of the inputs to that neuron.


One of the simplest ways to study the patterning of spike activity in a neuron is to record the spikes from a single neuron, using a fine microelectrode, and then to construct an interspike interval histogram. This is simply a plot of the distribution of the observed times between spikes (t1, t2, t3, etc)  collected in ‘bins’ of fixed width, say 1 ms. Typically, such a histogram would be constructed from about 2000 such intervals; if a neuron is firing at an average rate of about 5 spikes/s this will need a recording of 5-10 min of activity.
In this example, the neuron has quite a prolonged period of relative inexcitability after each spike, and so we might predict that this cell is one that shows a long [[hyperpolarsising after-potential]] (HAP) after each spike. For this particular cell, this is wholly correct; the cell is an oxytocin cell, and in these cells spikes trigger a large influx of calcium into the cell, and (in these cells) this causes a prolonged opening of a class of [[calcium-activated potassium channel]]s, and this produces a relatively long HAP.
[[Image:ISIH.png|thumb|300 px| Interspike interval distribution of the spontaneou activity of a typical magnocellular oxytocin neuron recorded from the rat supraoptic nucleus. The curve is a single negative exponential curve fitted to the tail of the histogram.]]
The figure on the right shows the interspike interval histogram recorded from a single neuron in the hypothalamus. Immediately after a spike, a neuron has an absolute refractory period in which it is unable to fire another spike, so the first few bins of the histogram will be empty – the histogram starts from zero. After this, the neuron has a relative refractory period, during which it is hard, but not impossible, to trigger another spike, and as this relative refractory period gradually decays, the interspike interval distribution rises to its peak value – the mode of the histogram, in this example at about 50 ms. The tail of the histogram (from about 50 ms on) declines exponentially to zero, as shown by the fitted line. This exponentially declining tail is an indication that, after about 50 ms after a spike, spikes are triggered by an essentially random process. This follows because the distribution of inter-event times for a wholly random process fits a single negative exponential, as first observed by Poisson.


In this example, we see that this particular neuron has quite a prolonged period of relative inexcitability after each spike, and might predict that this cell is one that shows a long hyperpolarsising after-potential (HAP) after each spike. For this particular cell, this is wholly correct; the cell is an oxytocin cell, and in these particular cells spikes trigger a large influx of calcium into the cell, and (in these particular cells) this subsequently causes a prolonged opening of a class of calcium-activated potassium channels, and this produces a relatively long HAP.
==Examples in recent papers==
 
* Witham CL, Baker SN (2007) Network oscillations and intrinsic spiking rhythmicity do not covary in monkey sensorimotor areas ''J Physiol'' [http://jp.physoc.org/cgi/content/full/580/3/801 508:801-13]
==External links==
* Zhang X, Carney LH (2005) Response properties of an integrate-and-fire model that receives subthreshold inputs ''Neural Comput''[http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=16212763 17:2571–601]
* [http://jp.physoc.org/cgi/content/full/580/3/801 A recent full paper]
* Sabatier N ''et al.'' (2004) Phasic spike patterning in rat supraoptic neurones in vivo and in vitro. ''J Physiol'' 558:161-80. PMID 15146047
* [http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=16212763 Another recent full paper]

Latest revision as of 05:58, 22 December 2010

This article is developing and not approved.
 Main Article
 Discussion
Related Articles  [?]
Bibliography  [?]
External Links  [?]
Citable Version  [?]
 
https://en.citizendium.org/wiki/index.php?title=Interspike_interval_histogram&printable=yes
This editable Main Article is under development and subject to a disclaimer.

An interspike-interval histogram is one of the ways by which experimental neurophysiologists analyse the electrical behaviour of neurons in the brain.

One of the simplest ways to study the patterning of spike activity in a neuron is to record the spikes from a single neuron, using a fine microelectrode, and then to construct an interspike interval histogram. This is simply a plot of the distribution of the observed times between spikes (t1, t2, t3, etc) collected in ‘bins’ of fixed width, say 1 ms. Typically, such a histogram would be constructed from about 2000 such intervals; if a neuron is firing at an average rate of about 5 spikes/s this will need a recording of 5-10 min of activity.

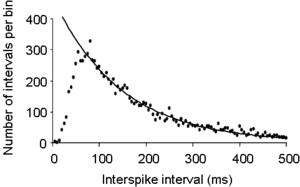
Interspike interval distribution of the spontaneous activity of a typical magnocellular oxytocin neuron recorded from the rat supraoptic nucleus. The curve is a single negative exponential curve fitted to the tail of the histogram.

The figure on the right shows the interspike interval histogram recorded from a single neuron in the hypothalamus. Immediately after a spike, a neuron has an absolute refractory period in which it is unable to fire another spike, so the first few bins of the histogram will be empty – the histogram starts from zero. After this, the neuron has a relative refractory period, during which it is hard, but not impossible, to trigger another spike, and as this relative refractory period gradually decays, the interspike interval distribution rises to its peak value – the mode of the histogram, in this example at about 50 ms. The tail of the histogram (from about 50 ms on) declines exponentially to zero, as shown by the fitted line. This exponentially declining tail is an indication that, after about 50 ms after a spike, spikes are triggered by an essentially random process. This follows because the distribution of inter-event times for a wholly random process fits a single negative exponential, as first observed by Poisson.

In this example, the neuron has quite a prolonged period of relative inexcitability after each spike, and so we might predict that this cell is one that shows a long hyperpolarsising after-potential (HAP) after each spike. For this particular cell, this is wholly correct; the cell is an oxytocin cell, and in these cells spikes trigger a large influx of calcium into the cell, and (in these cells) this causes a prolonged opening of a class of calcium-activated potassium channels, and this produces a relatively long HAP.

Examples in recent papers

  • Witham CL, Baker SN (2007) Network oscillations and intrinsic spiking rhythmicity do not covary in monkey sensorimotor areas J Physiol 508:801-13
  • Zhang X, Carney LH (2005) Response properties of an integrate-and-fire model that receives subthreshold inputs Neural Comput17:2571–601
  • Sabatier N et al. (2004) Phasic spike patterning in rat supraoptic neurones in vivo and in vitro. J Physiol 558:161-80. PMID 15146047
Retrieved from "https://citizendium.org/wiki/index.php?title=Interspike_interval_histogram&oldid=32942"