Right angle (geometry): Difference between revisions
Jump to navigation
Jump to search
imported>Miguel Adérito Trigueira (added missing part of demonstration, sp) |
imported>Miguel Adérito Trigueira (Re arranged existing contend, restored formatting) |
||
| Line 1: | Line 1: | ||
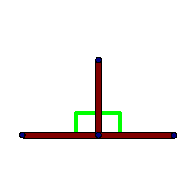
[[Image:Right angle (geometry) definition.png|frame|Diagram showing the definition of a right angle. The green parts are not part of the construction but show that the angles are both 90 degrees and equal to one another]] | [[Image:Right angle (geometry) definition.png|frame|Diagram showing the definition of a right angle. The green parts are not part of the construction but show that the angles are both 90 degrees and equal to one another]] | ||
In [[Euclidean geometry]], a '''right angle''', symbolized by the L-shaped figure '''∟''', is created when two straight lines meet perpendicularly at 90 degrees to each other | In [[Euclidean geometry]], a '''right angle''', symbolized by the L-shaped figure '''∟''', bisects the angle of the line into two equal parts. The right angle is created when two straight lines meet perpendicularly at 90 degrees to each other. | ||
The right angle | The right angle is demonstrated: | ||
Given a line DC with point B lying on it | |||
Project a line from B through point A | |||
Take B as the vertex of angle ABC | |||
If the angle ABC equals the angle ABD | |||
then angle ABC is a right angle, | |||
and so is angle ABD | |||
The | The plus sign, +, consists of two such lines, and so the four angles at its heart are all right angles. | ||
Revision as of 03:47, 21 August 2008
_definition.png)
Diagram showing the definition of a right angle. The green parts are not part of the construction but show that the angles are both 90 degrees and equal to one another
In Euclidean geometry, a right angle, symbolized by the L-shaped figure ∟, bisects the angle of the line into two equal parts. The right angle is created when two straight lines meet perpendicularly at 90 degrees to each other.
The right angle is demonstrated:
Given a line DC with point B lying on it Project a line from B through point A Take B as the vertex of angle ABC If the angle ABC equals the angle ABD then angle ABC is a right angle, and so is angle ABD
The plus sign, +, consists of two such lines, and so the four angles at its heart are all right angles.