Limit of a function: Difference between revisions
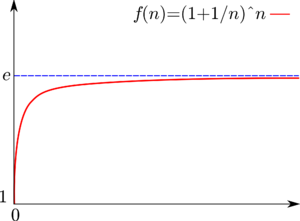
imported>Johan Förberg (Added graph of (1+ 1/n)^n) |
imported>Johan Förberg No edit summary |
||
| Line 7: | Line 7: | ||
:<math> \lim_{x \to a}f(x) = L </math> | :<math> \lim_{x \to a}f(x) = L </math> | ||
means that ''f''(''x'') can be made arbitrarily close to ''L'' by making ''x'' sufficiently close to ''a''. We say that "the limit of the function ''f'' of ''x'', as ''x'' approaches ''a'', is ''L''". | means that ''f''(''x'') can be made arbitrarily close to ''L'' by making ''x'' sufficiently close to ''a''. We say that "the limit of the function ''f'' of ''x'', as ''x'' approaches ''a'', is ''L''". This does not necessarily mean that ''f''(''a'') is equal to ''L'', or that the function is even defined at the point ''a''. | ||
Limit of a function can in some cases be defined even at values of the argument at which the function itself is not defined. For example, | Limit of a function can in some cases be defined even at values of the argument at which the function itself is not defined. For example, | ||
Revision as of 04:23, 2 October 2010
In mathematics, the concept of a limit is used to describe the behavior of a function as its argument either "gets close" to some point, or as it becomes arbitrarily large.
Suppose f(x) is a real-valued function and a is a real number. The expression
means that f(x) can be made arbitrarily close to L by making x sufficiently close to a. We say that "the limit of the function f of x, as x approaches a, is L". This does not necessarily mean that f(a) is equal to L, or that the function is even defined at the point a.
Limit of a function can in some cases be defined even at values of the argument at which the function itself is not defined. For example,
although the function
is not defined at x=0.
Formal definition
Let f be a function defined on an open interval containing a (except possibly at a) and let L be a real number.
means that
- for each real ε > 0 there exists a real δ > 0 such that for all x with 0 < |x − a| < δ, we have |f(x) − L| < ε.
This formal definition of function limit is due to the German mathematician Karl Weierstrass.