Cross product

The cross product, or vector product, is a type of vector multiplication in $\scriptstyle \mathbb {R} ^{3}$, and is widely used in many areas of mathematics and physics. In general Euclidean spaces there is another type of multiplication called the dot product (or scalar product). Both the dot product and the cross product are widely used in in the study of optics, mechanics, electromagnetism, and gravitational fields, for example.

Definition

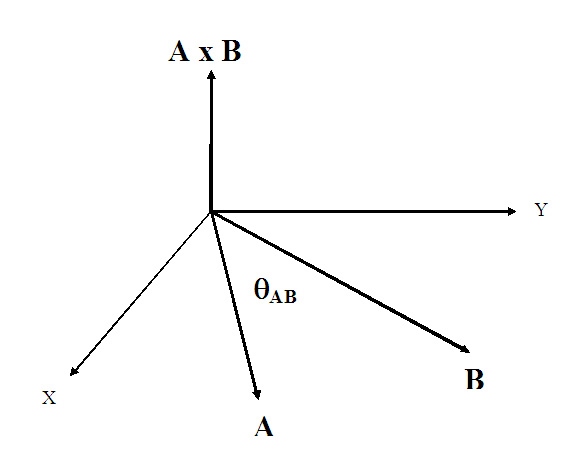
Given two vectors, A = (A_x,A_y,A_z) and B = (B_x,B_y,B_z) in $\mathbb {R} ^{3}$, the cross product is defined as the vector product of the magnitude of A, the magnitude of B, the sine of the smaller angle between them, and a unit vector (a_N) that is perpendicular (or normal to) the plane containing vectors A and B and which follows the right-hand rule (see below).

A x B = a_N |A||B|sinθ_AB

where $|\mathbf {A} |=(\mathbf {A} \cdot \mathbf {A} )^{1/2}$ and $|\mathbf {B} |=(\mathbf {B} \cdot \mathbf {B} )^{1/2}$ are, respectively, the magnitudes of A and B. See dot product for the evaluation of this equation.

Reversing the order of the vectors A and B results in a unit vector in the opposite direction, meaning that the cross product is not commutative, and thus:

B x A = -(A x B)

The cross product of any vector with itself (or another parallel vector) is zero because the sin(0) = 0.

A x A = 0

Another formulation

Rather than determining the angle and perpendicular unit vector to solve the cross product, the form below is often used to solve the cross product in $\mathbb {R} ^{3}$.

A x B = (A_yB_z - A_zB_y)a_x + (A_zB_x - A_xB_z)a_y + (A_xB_y - A_yB_x)a_z,

where a_x, a_y and a_z are the orthonormal bases on which A and B have been defined. The above formula can be written more concisely in the following form:

$\mathbf {A} \times \mathbf {B} =\left|{\begin{array}{ccc}\mathbf {a} _{x}&\mathbf {a} _{y}&\mathbf {a} _{z}\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{array}}\right|,$

where $\left|\cdot \right|$ denotes the determinant of a matrix.

The right hand rule

The diagram below illustrates the direction of A x B, which follows the right hand rule. If one points the fingers of the right hand towards the head of vector A (with the wrist at the origin), then curls them towards the direction of B, the extended thumb will point in the direction of A x B.

Vector Diagram illustrating the direction of A x B