Cross product: Difference between revisions
imported>Hendra I. Nurdin mNo edit summary |
imported>David E. Volk (Add CrossProduct.jpg Image) |
||
| Line 39: | Line 39: | ||
where <math>\left|\cdot\right|</math> denotes the determinant of a matrix. | where <math>\left|\cdot\right|</math> denotes the determinant of a matrix. | ||
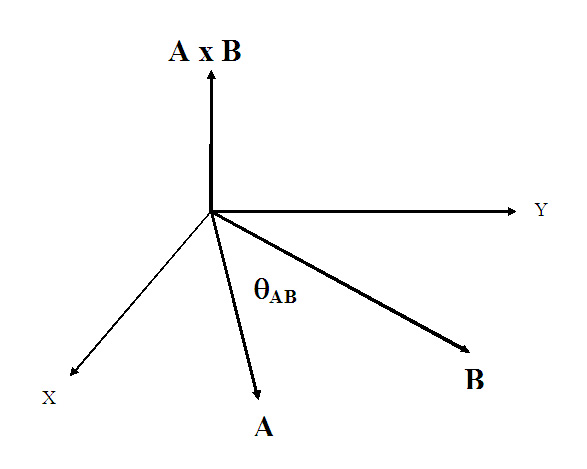
[[Image:CrossProduct.jpg|center|frame|Vector Diagram illustrating the direction of A x B]] | |||
[[Category:CZ Live]] | [[Category:CZ Live]] | ||
[[Category:Physics Workgroup]] | [[Category:Physics Workgroup]] | ||
[[Category:Mathematics Workgroup]] | [[Category:Mathematics Workgroup]] | ||
Revision as of 10:29, 10 October 2007
The cross product, or vector product, is a type of vector multiplication in , and is widely used in many areas of mathematics and physics. In general Euclidean spaces there is another type of multiplication called the dot product ( or scalar product). Both the dot product and the cross product are widely used in in the study of optics, mechanics, electromagnetism, and gravitational fields, for example.
Definition
Given two vectors, A = (Ax,Ay,Az) and B = (Bx,By,Bz) in , the cross product is defined as the vector product of the magnitude of A, the magnitude of B, the sine of the smaller angle between them, and a unit vector (aN) that is perpendicular (or normal to) the plane containing vectors A and B and which follows the right-hand rule (see below).
A x B = aN |A||B|sinθAB
where and are, respectively, the magnitudes of A and B. See dot product for the evaluation of this equation.
Reversing the order of the vectors A and B results in a unit vector in the opposite direction, meaning that the cross product is not commutative, and thus:
B x A = -(A x B)
The cross product of any vector with itself (or another parallel vector) is zero because the sin(0) = 0.
A x A = 0
Another formulation
Rather than determining the angle and perpendicular unit vector to solve the cross product, the form below is often used to solve the cross product in .
A x B = (AyBz - AzBy)ax + (AzBx - AxBz)ay + (AxBy - AyBx)az,
where ax, ay and az are the orthonormal bases on which A and B have been defined. The above formula can be written more concisely in the following form:
where denotes the determinant of a matrix.