User:John R. Brews/Draft

(PD) Image: John R. Brews
Fermi occupancy function vs. energy departure from Fermi level in volts for three temperatures; degeneracy factor g ≡ 1.

Fermi function

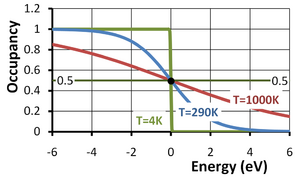
The Fermi function or, more completely, the Fermi-Dirac distribution function describes the occupancy of a electronic energy level in a system of electrons at equilibrium. The occupancy f(E) of an energy level of energy E at an absolute temperature T in kelvins is given by:

${\begin{aligned}f(E)&={\frac {1}{1+\exp \left({\frac {E-E_{F}}{k_{B}T}}\right)}}\\&={\frac {1}{1+\exp \left({\frac {(E-E_{F})/q}{k_{B}T/q}}\right)}}\\\end{aligned}}$

Here E_F is called the Fermi energy and k_B is the Boltzmann constant. This occupancy function is plotted in the figure versus the energy E−E_F in eV (electron volts). From the second form of the function above, it can be seen that the "natural" unit of energy is the thermal voltage k_BT/q; as temperature increases, so does this unit, accounting for the stretching out of the function along the energy axis with increasing temperature.

Notice that for an energy level with E = E_F and a degeneracy factor g = 1, the occupancy is 1/2 regardless of temperature. The Fermi level E_F thus can be referred to as the half-occupancy level.

Dopant levels

Dopant impurities are used in semiconductors to adjust the conductivity of the material. They introduce energy levels for electrons, and if they are acceptors become negatively charged when occupied. Suppose energies are measured from the valence band edge in a semiconductor, so the impurity energy level becomes E_a,d = E−E_V and E_F is replaced by E_F − E_V. Then the occupancy of the impurity level is given by:

$f(E_{a,d})={\frac {1}{1+g(E_{a,d})\exp \left({\frac {E_{a,d}-E_{F}}{k_{B}T}}\right)}}\ ,$

where g is the so-called degeneracy factor. The origin of the degeneracy factor goes back to the underlying derivation of the Fermi function, which is fundamentally a determination of the most probable way n-electrons can be distributed among N energy levels while constrained by a fixed energy for the ensemble. In this counting of permutations, the contribution of the impurities is included by making some basic assumptions about the impurity behavior that are essentially empirical in nature. For example, one may postulate that the impurity atoms divide into two populations, one with n_i electrons and the other with n_i+1 electrons. Moreover, we suppose that the electrons on any one atom in the first population may fall into any of g₀ possible equivalent levels, while for those in the second population there are g₁ possible levels. Then the degeneracy factor in the Fermi occupancy function is found to be g₀/g₁.

Typically an acceptor provides an energy level related to the valence band structure of the host material. A common case is two levels, one from the "heavy" hole valence band and one from the "light" hole valence band. Thus, the number of negatively charge acceptors, compared to the total number of acceptors, is:

${\frac {N_{a}^{-}}{N_{a}}}={\frac {1}{1+4\exp \left({\frac {E_{a}-E_{F}}{k_{B}T}}\right)}}\ ,$

where the degeneracy factor of 4 stems from the possibility of either a spin-up or a spin-down electron occupying the level E_a, and the existence of two sources for holes of energy E_a, one from the "heavy" hole band and one from the "light" hole band.

In contrast to acceptors, donors become positively charged and tend to give up an electron. The number of positive donors compared to the total number of donors is then:

${\frac {N_{d}^{+}}{N_{d}}}={\frac {1}{1+2\exp \left({\frac {E_{d}-E_{F}}{k_{B}T}}\right)}}\ ,$

where now the degeneracy factor is 2 (because of the spin-up or spin-down possibilities for occupancy) and there is typically only one energy level E_d associated with the conduction band.

Fermi level

The Fermi level or Fermi energy, E_F, in the Fermi function represents for a system of independent electrons a very special case of the more general notion of an electrochemical potential. The chemical potential of a chemical species is the work required to add a particle of that species to an ensemble of particles at constant temperature and pressure. The electrochemical potential is the same quantity, but for a charged particle that has both chemical and electrical interactions.

For a system of independent electrons, this energy is the Fermi energy.

Fermi surface

(PD) Image: John R. Brews
Fermi surface in k-space for a nearly filled band in the face-centered cubic lattice

At zero temperature, the energy levels up to the Fermi energy are full, and those below are empty. For an assembly of particles occupying these energy levels, the equation E = E_F defines a surface in the space of parameters determining the energy, such as the particle momentum. This surface, separating the filled from the empty energy levels, is called the Fermi surface.

For example, for an ideal "gas" of independent electrons, the energy of an electron in the gas is given by:

$E={\frac {(\hbar \mathbf {k} )^{2}}{2m}}\ ,$

where m is the electron mass, and the wavevector k is related to momentum p by p = ћk, where ћ is Planck's constant divided by 2π. The wavevector is related to the de Boglie wavelength of the particle.

For this ideal electron gas, the equation E = E_F defines a spherical surface in the space of the wavevector. The energy of an electron in a solid is a more complicated function of the wavevector k. In a crystal, far from being spherical, the Fermi surface can be complex indeed.