User:John R. Brews/Draft: Difference between revisions
imported>John R. Brews |
imported>John R. Brews |
||
| Line 4: | Line 4: | ||
==Fermi function== | ==Fermi function== | ||
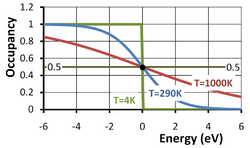
{{Image|Fermi function.PNG|right|250px|Fermi occupancy function ''vs''. energy in thermal units for three temperatures.}} | {{Image|Fermi function.PNG|right|250px|Fermi occupancy function ''vs''. energy in thermal units for three temperatures.}} | ||
The '''Fermi function''' or, more completely, the '''Fermi-Dirac distribution function''' describes the occupancy of a electronic energy level in a system of electrons at equilibrium. The occupancy ''f(E)'' of an energy level of energy ''E'' at an [[absolute temperature]] ''T'' is given by: | The '''Fermi function''' or, more completely, the '''Fermi-Dirac distribution function''' describes the occupancy of a electronic energy level in a system of electrons at equilibrium. The occupancy ''f(E)'' of an energy level of energy ''E'' at an [[absolute temperature]] ''T'' in [[Kelvin (unit)|kelvin]]s is given by: | ||
:<math>f(E) = \frac{1}{1+g(E)\exp\left(\frac {E-E_F}{k_B T}\right )} \ , </math> | :<math>f(E) = \frac{1}{1+g(E)\exp\left(\frac {E-E_F}{k_B T}\right )} \ , </math> | ||
Revision as of 12:03, 13 January 2011
Fermi function
The Fermi function or, more completely, the Fermi-Dirac distribution function describes the occupancy of a electronic energy level in a system of electrons at equilibrium. The occupancy f(E) of an energy level of energy E at an absolute temperature T in kelvins is given by:
where g(E) is the degeneracy of the energy level, that is, the number of quantum states with that particular energy. Here EF is called the Fermi energy and kB is the Boltzmann constant.
Notice that for an energy level with E = EF and a degeneracy factor g = 1, the occupancy is 1/2. The Fermi level EF thus can be referred to as the half-occupancy level.
Dopant levels
Dopant impurities are used in semiconductors to adjust the conductivity of the material. They introduce energy levels for electrons, and if they are acceptors become negatively charged when occupied. Typically an acceptor provides an energy level related to the valence band structure of the host material. A common case is two levels, one from the "heavy" hole valence band and one from the "light" hole valence band. Thus, the number of negatively charge acceptors, compared to the total number of acceptors, is:
where the degeneracy factor of 4 stems from the possibility of either a spin-up or a spin-down electron occupying the level E, and the existence of two sources for holes of energy E, one from the "heavy" hole band and one from the "light" hole band.
In contrast to acceptors, donors become positively charged and tend to give up an electron. The number of positive donors compared to the total number of donors is then:
where now the degeneracy factor is 2 (because of the spin-up or spin-down possibilities for occupancy) and there is typically only one energy level associated with the conduction band.[1][2][3][4][5]
Fermi level
The Fermi level in the Fermi function represents for a system of independent electrons a very special case of the more general notion of an electrochemical potential. The chemical potential of a chemical species is the work required to add a particle of that species to an ensemble of particles at constant temperature and pressure. The electrochemical potential is the same quantity, but for a charged particle that has both chemical and electrical interactions.[6]
For a system of independent electrons, this energy is the Fermi energy.